在WEB中使平面元素实现三维动画

观察点

使用过3d引擎的都会比较熟悉，几乎所有的3d引擎都有一个摄像机（观察点）的概念。观察点则是判断物体远近关系的依据，也是实现三维视觉的关键。

想象一下，现在有一个拖离电脑屏幕的矩形BGED，通过观察点A所在屏幕上看到的形状应该是CHFO，如下图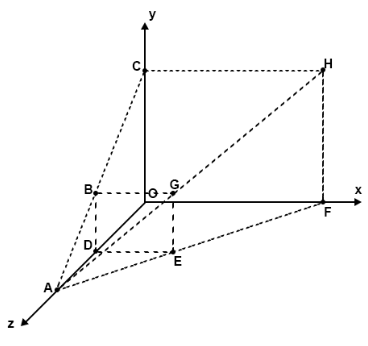

（图片来自网络）

旋转动画

transform: perspective

我们设置的一些css动画都是以平面形式展示的，原因是我们“离屏幕”太近了。我们可以加上transform: perspective(100px)这个属性，也就是观察这个动画的位置（z轴）的距离为100px，效果如下：

Svg中的实现

有些时候我们想让一些奇形怪状的平面图形也拥有三维空间感，我们继续分析一下，还是上面那张图
对于空间内任意位置，我们都可以看成是在z轴上的某一点A(0，0，zA)，先经历一次x轴方向的平移（此时投影H的y坐标不变），再经历一次y轴方向的平移（此时投影H的x坐标不变），平移之前点A观察到点G的投影H坐标可表示为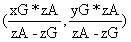 对其进行x轴方向的平移，（此时投影H的y坐标不变），H的坐标可表示为 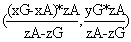再对其进行y轴方向的平移，（此时投影H的x坐标不变），H的坐标可表示为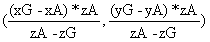
（图片来自网络）

    const visual = {
        x: 150,
        y: 150,
        z: 300
      }

      function transformCoordinatePoint(x, y, z, offsetX = 300, offsetY = 300) {
        return [(x - visual.x) * visual.z / (visual.z - z) + offsetX,
        (y - visual.y) * visual.z / (visual.z - z) + offsetY
        ]
      }

      function getPathStr(path) {
        return [0, 2, 4, 1, 3, 0].map((step, i) => {
          return (i === 0 ? 'M' : 'L') + path[step].join(',')
        }).join(' ') + 'Z'
      }

      // root.a(svg);
      function drawAnimation() {
        let rotationAngle = 1
        window.requestAnimationFrame(() => {
          paths = paths.map(item => {
            let x = item[0]
            let y = item[1]
            let z = item[2]
            // 变换后的x坐标
            item[0] = x * Math.cos(rotationAngle / 180 * Math.PI) - z * Math.sin(rotationAngle / 180 * Math.PI)
            // 绕y轴旋转，y左边不会发生变化
            item[1] = y
            // 变换后的z坐标
            item[2] = z * Math.cos(rotationAngle / 180 * Math.PI) + x * Math.sin(rotationAngle / 180 * Math.PI)
            return item
          });
          const viewPaths = paths.map(item => transformCoordinatePoint(item[0], item[1], item[2]))
          path2.setAttribute('d', getPathStr(viewPaths))
          drawAnimation()
        })
      }

      drawAnimation()